 TRIGONOMETRIC FUNCTIONS
TRIGONOMETRIC FUNCTIONS TRIGONOMETRIC FUNCTIONS
TRIGONOMETRIC FUNCTIONS
Recall that a real number ![]() can be interpreted as
the measure of the angle constructed as follows: wrap a piece of
string of length
can be interpreted as
the measure of the angle constructed as follows: wrap a piece of
string of length ![]() units around the unit circle
units around the unit circle ![]() (counterclockwise if
(counterclockwise if ![]() , clockwise if
, clockwise if ![]() ) with
initial point P(1,0) and terminal point Q(x,y). This gives rise to
the central angle with vertex O(0,0) and sides through the points
P
and Q.
All six trigonometric functions of
) with
initial point P(1,0) and terminal point Q(x,y). This gives rise to
the central angle with vertex O(0,0) and sides through the points
P
and Q.
All six trigonometric functions of ![]() are defined in terms of
the coordinates of the point Q(x,y), as follows:
are defined in terms of
the coordinates of the point Q(x,y), as follows:
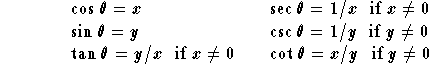
Since Q(x,y) is a point on the unit circle, we know that
![]() . This fact and the definitions of the trigonometric
functions give rise to the following fundamental identities:
. This fact and the definitions of the trigonometric
functions give rise to the following fundamental identities:

This modern notation for trigonometric functions is due to L. Euler (1748).
More generally, if Q(x,y) is the point where the circle
![]() of radius R is intersected by the angle
of radius R is intersected by the angle ![]() , then
it follows (from similar triangles) that
, then
it follows (from similar triangles) that
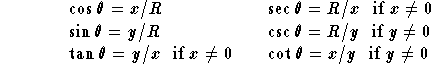
Periodic Functions
If an angle ![]() corresponds to a point Q(x,y) on the unit
circle, it is not hard to see that the angle
corresponds to a point Q(x,y) on the unit
circle, it is not hard to see that the angle ![]() corresponds
to the same point Q(x,y), and hence that
corresponds
to the same point Q(x,y), and hence that
Moreover, ![]() is the smallest positive angle for which
Equations 1 are true for any angle
is the smallest positive angle for which
Equations 1 are true for any angle ![]() .
In general, we have for all angles
.
In general, we have for all angles ![]() :
:
We call the number ![]() the period of the trigonometric
functions
the period of the trigonometric
functions ![]() and
and ![]() , and refer to these functions as being
periodic. Both
, and refer to these functions as being
periodic. Both ![]() and
and ![]() are periodic functions as well,
with period
are periodic functions as well,
with period ![]() , while
, while ![]() and
and ![]() are periodic with period
are periodic with period
![]() .
.
EXAMPLE 1
Find the period of the function ![]() .
.
Solution:
The function ![]() runs through a full cycle
when the angle 3x runs from 0 to
runs through a full cycle
when the angle 3x runs from 0 to ![]() , or equivalently when x
goes from 0 to
, or equivalently when x
goes from 0 to ![]() . The period of f(x) is then
. The period of f(x) is then ![]() .
.
EXERCISE 1
Find the period of the function ![]() .
.
Consider the triangle with sides of length ![]() and hypotenuse
c>0 as in Figure 1 below:
and hypotenuse
c>0 as in Figure 1 below:
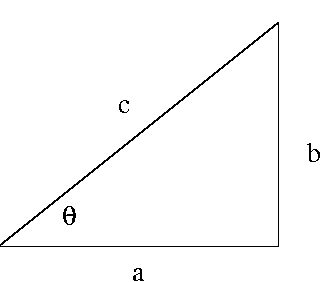
|
| Figure 1 |
For the angle ![]() pictured in the figure,
we see that
pictured in the figure,
we see that
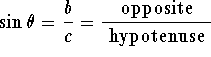 | 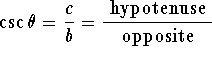 |
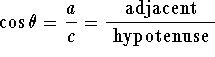 | 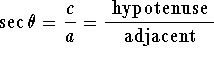 |
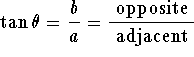 | 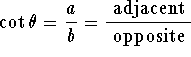 |
There are a few angles for which all trigonometric functions may be found using the triangles shown in the following Figure 2.
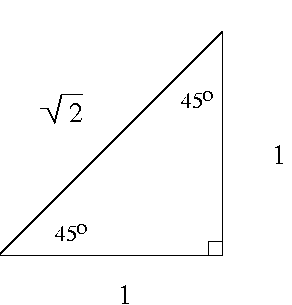
|
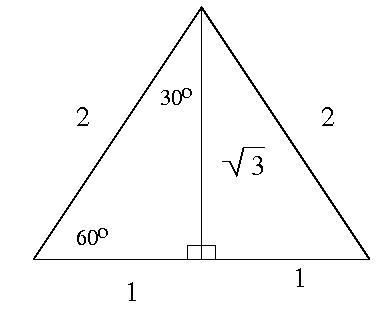
|
| Figure 2 |
This list may be extended with the use of reference angles (see Example 2 below).
EXAMPLE 1:
Find the values of all trigonometric functions of the angle
![]() .
.
Solution:
From Figure 2, we see that the angle of ![]() corresponds to the point
corresponds to the point ![]() on the unit circle, and
so
on the unit circle, and
so
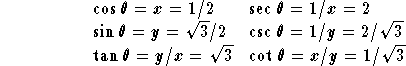
EXAMPLE 2:
Find the values of all trigonometric functions of the angle
![]() .
.
Solution:
Observe that an angle of ![]() is equivalent to 8
whole revolutions (a total of
is equivalent to 8
whole revolutions (a total of ![]() ) plus
) plus ![]() , Hence the
angles
, Hence the
angles ![]() and
and ![]() intersect the unit circle at the
same point Q(x,y), and so their trigonometric functions are the
same. Furthermore, the angle of
intersect the unit circle at the
same point Q(x,y), and so their trigonometric functions are the
same. Furthermore, the angle of ![]() makes an angle of
makes an angle of ![]() with respect to the x-axis (in the second quadrant). From this we can
see that
with respect to the x-axis (in the second quadrant). From this we can
see that ![]() and hence that
and hence that
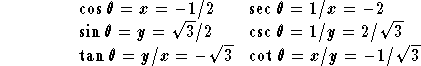
We call the auxiliary angle of ![]() the reference angle of
the reference angle of
![]() .
.
EXAMPLE 3
Find all trigonometric functions of an angle ![]() in the third
quadrant for which
in the third
quadrant for which ![]() .
.
Solution: We first construct a point R(x,y) on the terminal side of
the angle ![]() , in the third quadrant. If R(x,y) is such a point,
then
, in the third quadrant. If R(x,y) is such a point,
then ![]() and we see that we may take x=-5 and
R=6. Since
and we see that we may take x=-5 and
R=6. Since ![]() we find that
we find that
![]() (the negative signs on x and y are
taken so that R(x,y) is a point on the third quadrant, see
Figure 3).
(the negative signs on x and y are
taken so that R(x,y) is a point on the third quadrant, see
Figure 3).
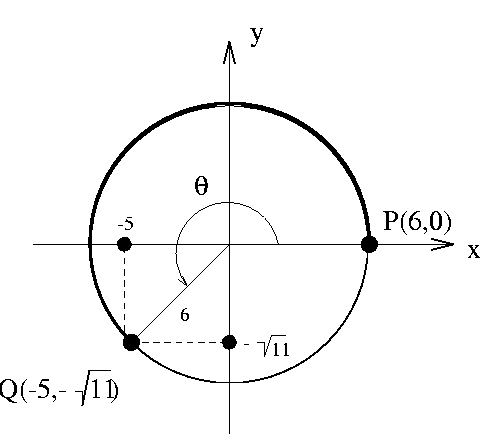
|
| Figure 3 |
It follows that
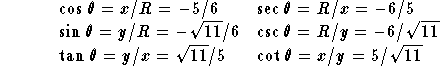
Here are some Exercises on the evaluation of trigonometric functions.
EXERCISE 2
EXERCISE 3
From a 200-foot observation tower on the beach, a man
sights a whale in difficulty. The angle of depression of the whale is
![]() . How far is the whale from the shoreline?
. How far is the whale from the shoreline?

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Luis Valdez Sanchez