TRIGONOMETRY - MEASURE OF AN ANGLETRIGONOMETRY - MEASURE OF AN ANGLE
Any real number 
may be interpreted as the radian measure of
an angle as follows: If 
, think of wrapping a length
of string around the standard unit circle C in the plane,
with initial point P(1,0), and proceeding counterclockwise around the
circle; do the same if 
, but wrap the string clockwise
around the circle. This process is described in Figure 1 below.
|
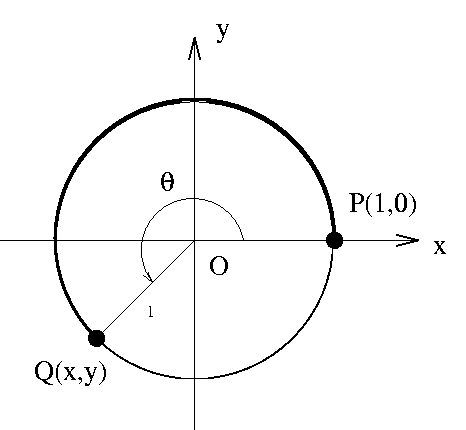
| Figure 1 |
If Q(x,y) is the point on the circle where the string ends,
we may think of as being an angle by associating to it the
central angle with vertex O(0,0) and sides passing through the points
P and Q.
If instead of wrapping a length s of string around the unit circle,
we decide to wrap it around a circle of radius R, the angle
(in radians) generated in the process will satisfy the following
relation:
Observe that the length s of string gives the measure of the angle
only when R=1.
As a matter of common practice and convenience, it is useful to
measure angles in degrees, which are defined by partitioning one
whole revolution into 360 equal parts, each of which is then called
one degree. In this way, one whole revolution around the unit circle
measures 
radians and also 360 degrees (or 
), that is:
Each degree may be further subdivided into 60 parts, called minutes, and in turn each minute may be subdivided into another 60 parts, called seconds:
EXAMPLE 1
Express the angle 
in Degree-Minute-Second (DMS)
notation.
Solution: We use Equation 3 to convert a fraction of a degree into minutes and a fraction of a minute into seconds:
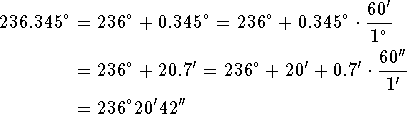
Therefore, 
.
EXAMPLE 2 Express the angle in radians.
Solution: From Equation 2 we see that
EXAMPLE 3 Find the length of an arc on a circle of radius 75
inches that spans a central angle of measure 
.
Solution: We use Equation 1, 
, with R=75
inches and
, to obtain
Here are some more exercises in the use of the rules given in Equations 1,2, and 3.
EXERCISE 1
Express the angle 
radians in (a) decimal form and (b) DMS
form.
EXERCISE 2
Express the angle 
in radians.
EXERCISE 3
Assume that City A and City B are located on the same
meridian in the Northern hemisphere and that the earth is a sphere of
radius 4000 mi.
The latitudes of City A and City B are
and 
, respectively.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Luis Valdez Sanchez
