 Hyperbolic Functions
Hyperbolic Functions Hyperbolic Functions
Hyperbolic FunctionsThe hyperbolic functions enjoy properties similar to the trigonometric functions; their definitions, though, are much more straightforward:
![]()
![]()
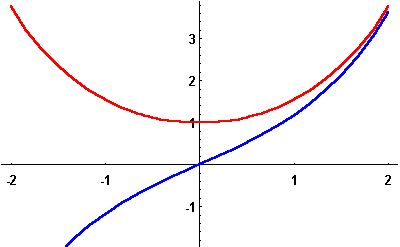
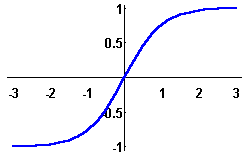
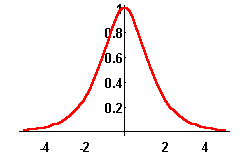
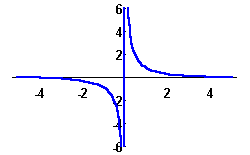
Here are their graphs: the ![]() (pronounce: "kosh") is pictured in red, the
(pronounce: "kosh") is pictured in red, the ![]() function (rhymes with the "Grinch") is depicted in blue.
function (rhymes with the "Grinch") is depicted in blue.
|
As their trigonometric counterparts, the ![]() function is even, while the
function is even, while the ![]() function is odd.
function is odd.
Their most important property is their version of the Pythagorean Theorem.
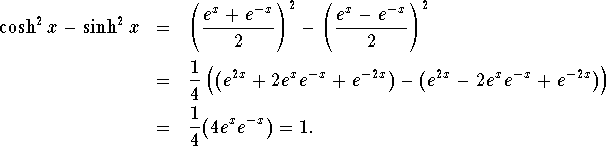
While ![]() ,
, ![]() , parametrizes the unit circle, the hyperbolic functions
, parametrizes the unit circle, the hyperbolic functions ![]() ,
, ![]() , parametrize the standard hyperbola
, parametrize the standard hyperbola ![]() , x>1.
, x>1.
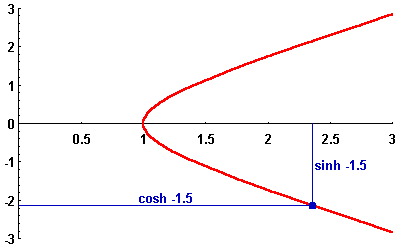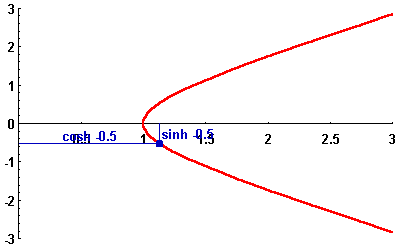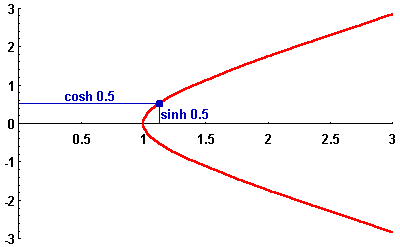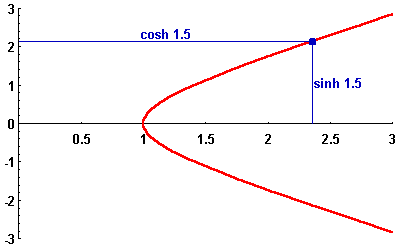
In the picture below, the standard hyperbola is depicted in red, while the point ![]() for various values of the parameter t is pictured in blue.
for various values of the parameter t is pictured in blue.
|
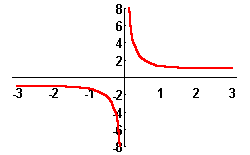
The other hyperbolic functions are defined the same way, the rest of the trigonometric functions is defined:
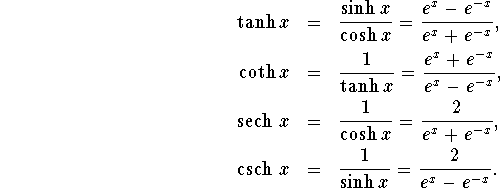
|
|
|
|
For every formula for the trigonometric functions, there is a similar (not necessary identical) formula for the hyperbolic functions:
Let's consider for example the addition formula for the hyperbolic cosine function:
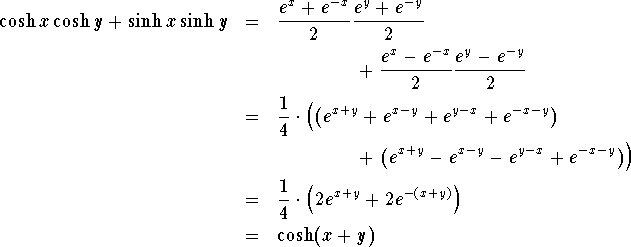
Show that ![]() .
.
Here is the answer.
Click here to go to the inverse hyperbolic functions.
Helmut Knaust