 Inverse Hyperbolic Functions
Inverse Hyperbolic Functions Inverse Hyperbolic Functions
Inverse Hyperbolic Functions
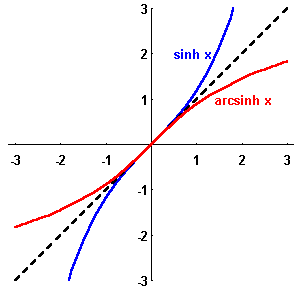
The hyperbolic sine function is a one-to-one function, and thus has an inverse. As usual, we obtain the graph of the inverse hyperbolic sine function ![]() (also denoted by
(also denoted by ![]() ) by reflecting the graph of
) by reflecting the graph of ![]() about the line y=x:
about the line y=x:
|
Since ![]() is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
is defined in terms of the exponential function, you should not be surprised that its inverse function can be expressed in terms of the logarithmic function:
Let's set ![]() , and try to solve for x:
, and try to solve for x:
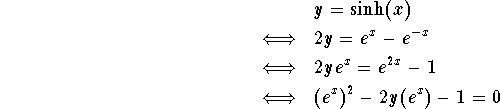
This is a quadratic equation with ![]() instead of x as the variable. y will be considered a constant.
instead of x as the variable. y will be considered a constant.
So using the quadratic formula, we obtain
![]()
Since ![]() for all x, and since
for all x, and since ![]() for all y, we have to discard the solution with the minus sign, so
for all y, we have to discard the solution with the minus sign, so
![]()
and consequently
![]()
Read that last sentence again slowly!
We have found out that
|
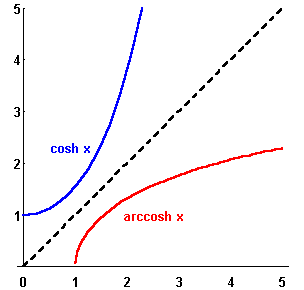
Here it is: Express the inverse hyperbolic cosine functions in terms of the logarithmic function!
Click here to see the answer, and to continue.