

Consider the Hermite Equation of order 5:
y''-2ty'+10y=0.
Find the solution satisfying the initial conditions a0=1, a1=0.
The solution will not be a polynomial.
Since a1=0, all odd coefficients will be zero.
Let's compute a few of the even coefficients:
From this it is not too hard to come up with the general formula:
This leads to the formula
for the solution to the given initial value problem.
The solution converges and solves the equation for all real numbers.

[Back]
[Exercises]
[Next]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Helmut Knaust
1998-07-08
Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour



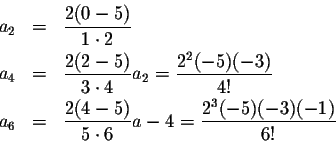
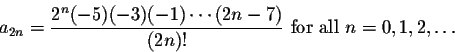
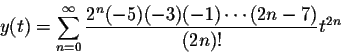

 S.O.S MATHematics home page
S.O.S MATHematics home page 