

Hermite's Equation of order k has the form
y''-2ty'+2ky=0,
where k is usually a non-negative integer.
We know from the previous section that this equation will have series solutions which both converge and solve the differential equation everywhere.
Hermite's Equation is our first example of a differential equation, which has a polynomial solution.
As usual, the generic form of a power series is
We have to determine the right choice for the coefficients (an).
As in other techniques for solving differential equations, once we have a "guess" for the solutions, we plug it into the differential equation.
Recall that
and
Plugging this information into the differential equation we obtain:
or after rewriting slightly:
Next we shift the first summation up by two units:
Before we can combine the terms into one sum, we have to overcome another slight obstacle: the second summation starts at n=1, while the other two start at n=0.
Evaluate the 0th term for the second sum:
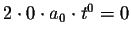 .
Consequently, we do not change the value of the second summation, if we start at n=0 instead of n=1:
.
Consequently, we do not change the value of the second summation, if we start at n=0 instead of n=1:
Thus we can combine all three sums as follows:
Therefore our recurrence relations become:
After simplification, this becomes
Let us look at the special case, where k=5, and the initial conditions are given as
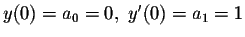 .
In this case, all even coefficients will be equal to zero, since a0=0 and each coefficient is a multiple of its second predecessor.
.
In this case, all even coefficients will be equal to zero, since a0=0 and each coefficient is a multiple of its second predecessor.
What about the odd coefficients? a1=1, consequently
and
What about a7:
Since a7=0, all odd coefficients from now on
will be equal to zero, since each coefficient is a multiple of its second predecessor.
Consequently, the solution has only 3 non-zero coefficients, and hence is a polynomial. This polynomial
(or a multiple of this polynomial) is called the Hermite Polynomial of order 5.
It turns out that the Hermite Equation of positive integer order k always has a polynomial solution of order k. We can even be more precise: If k is odd, the initial value problem
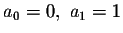 will have a polynomial solution, while for k even, the initial value problem
will have a polynomial solution, while for k even, the initial value problem
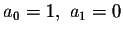 will have a polynomial solution.
will have a polynomial solution.
Find the Hermite Polynomials of order 1 and 3.
Find the Hermite Polynomials of order 2, 4 and 6.
Consider the Hermite Equation of order 5:
y''-2ty'+10y=0.
Find the solution satisfying the initial conditions a0=1, a1=0.

[Back]
[Next]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Helmut Knaust
1998-07-08
Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour



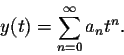
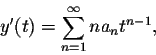
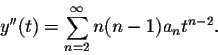
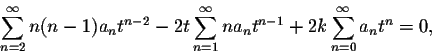
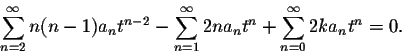
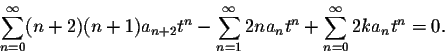
![]() .
Consequently, we do not change the value of the second summation, if we start at n=0 instead of n=1:
.
Consequently, we do not change the value of the second summation, if we start at n=0 instead of n=1:
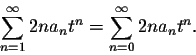
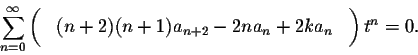
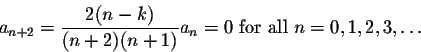
![]() will have a polynomial solution, while for k even, the initial value problem
will have a polynomial solution, while for k even, the initial value problem
![]() will have a polynomial solution.
will have a polynomial solution.

 S.O.S MATHematics home page
S.O.S MATHematics home page 