Reduction of Order Technique
Reduction of Order Technique
This technique is very important since it helps one to find a second
solution independent from a known one. Therefore, according to the
previous section, in order to find the general solution to
y'' + p(x)y' + q(x)y = 0, we need only to find one (non-zero)
solution, 
.
Let be a non-zero solution of
Then, a second solution 
independent of can be found as
Easy calculations give
,
where C is an arbitrary non-zero constant. Since we are looking for a second solution one may take C=1, to get
Remember that this formula saves time. But, if you forget it you
will have to plug 
into the equation to determine v(x)
which may lead to mistakes !
The general solution is then given by
Example: Find the general solution to the Legendre equation
,
using the fact that 
is a solution.
Solution: It is easy to check that indeed
is a solution. First, we need to rewrite the equation in the
explicit form
We may try to find a second solution 
by plugging it into the equation. We leave it to the reader to
do that! Instead let us use the formula
Techniques of integration (of rational functions) give
,
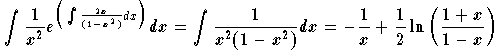which gives
The general solution is then given by
Remark: The formula giving can be obtained by also
using the
properties of the Wronskian (see also the discussion on the Wronskian).
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi