Linear Independence and the Wronskian

Let and be two differentiable functions. The Wronskian , associated to and , is the function

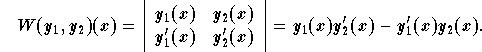
For a discussion on the motivation behind the Wronskian, click HERE.

We have the following important properties:

(1)

If and are two solutions of the equation y'' + p(x)y' + q(x)y = 0, then

(2)

If and are two solutions of the equation y'' + p(x)y' + q(x)y = 0, then

In this case, we say that and are linearly independent.

(3)

If and are two linearly independent solutions of the equation y'' + p(x)y' + q(x)y = 0, then any solution y is given by

for some constant and . In this case, the set is called the fundamental set of solutions.

Example: Let be the solution to the IVP

and be the solution to the IVP

Find the Wronskian of . Deduce the general solution to

Solution: Let us write . We know from the properties that

$$W(x) = W(0) e^{\displaystyle - \int_0^x (2t-1)dt} = W(0) e^{\displaystyle -x^2 + x}\;.$$

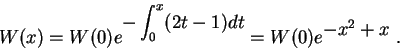
Let us evaluate W(0). We have

Therefore, we have

Since , we deduce that is a fundamental set of solutions. Therefore, the general solution is given by

,

where are arbitrary constants.

[Differential Equations] [First Order D.E.] [Second Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour