Factoring and Roots of Polynomials
Factoring and Roots of Polynomials
If you write a polynomial as the product of two or more polynomials, you have factored the polynomial. Here is an example:
The polynomials x-3 and 
are called factors of the polynomial 
. Note that the degrees of the factors, 1 and 2, respectively, add up to the degree 3 of the polynomial we started with. Thus factoring breaks up a complicated polynomial into easier, lower degree pieces.
We are not completely done; we can do better: we can factor
We have now factored the polynomial into three linear (=degree 1) polynomials. Linear polynomials are the easiest polynomials. We can't do any better. Whenever we cannot factor any further, we say we have factored the polynomial completely.
Once again consider the polynomial
Let's plug in x=3 into the polynomial.
Consequently x=3 is a root of the polynomial .
Note that (x-3) is a factor of .
Let's plug in 
into the polynomial:
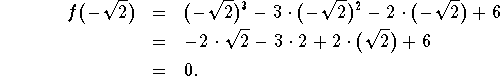
Thus, is a root of the polynomial .
Note that 
is a factor of .
Since we have already factored
there is an easier way to check that x=3 and are roots of f(x), using the right-hand side:
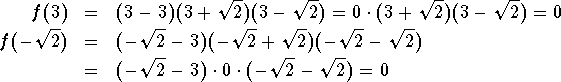
Does this work the other way round?
Let's look at an example: consider the polynomial 
. Note that x=2 is a root of f(x), since
Is (x-2) a factor of ? You bet!
We can check this by using long polynomial division:
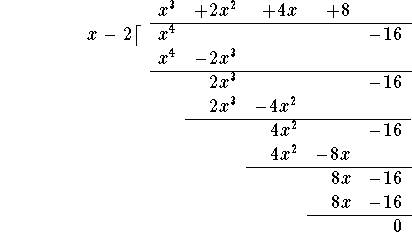
So we can factor
Let's sum up: Finding a root x=a of a polynomial f(x) is the same as having (x-a) as a linear factor of f(x). More precisely:
Given a polynomial f(x) of degree n, and a number a, then
if and only if there is a polynomial q(x) of degree n-1 so that
. Note that f(-2)=0.
completely. Note that 
and 
.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Helmut Knaust