 The magic identity
The magic identity The magic identity
The magic identity
Trigonometry is the art of doing algebra over the circle. So it is a mixture of algebra and geometry. The sine and cosine functions are just the coordinates of a point on the unit circle. This implies the most fundamental formula in trigonometry (which we will call here the magic identity)
![]()
where ![]() is any real number (of course
is any real number (of course ![]() measures an angle).
measures an angle).
Example. Show that
![]()
Answer. By definitions of the trigonometric functions we have
![]()
Hence we have
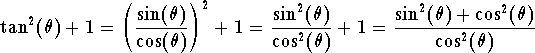
Using the magic identity we get
![]()
This completes our proof.
Remark. the above formula is fundamental in many ways. For example, it is very useful in techniques of integration.
Example. Simplify the expression
![]()
Answer. We have by definition of the trigonometric functions
![]()
Hence
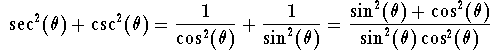
Using the magic identity we get
![]()
Putting stuff together we get
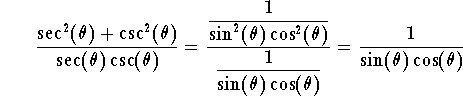
This gives
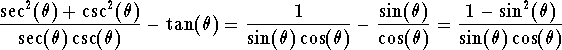
Using the magic identity we get
![]()
Therefore we have
![]()
Example. Check that
![]()
Example. Simplify the expression
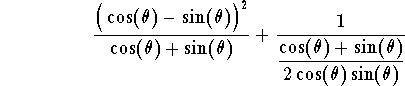
The following identities are very basic to the analysis of trigonometric expressions and functions. These are called Fundamental Identities
Reciprocal identities
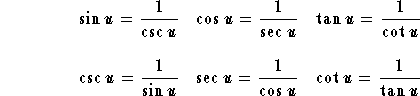
Pythagorean Identities
![]()
Quotient Identities
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi