Double-Angle and Half-Angle Formulas Double-Angle and Half-Angle Formulas
Double-Angle and Half-Angle formulas are very useful. For example, rational functions of sine and cosine wil be very hard to integrate without these formulas. They are as follow
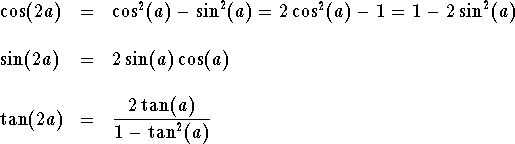
Example. Check the identities
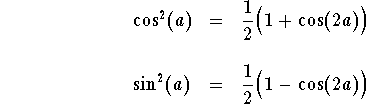
Answer. We will check the first one. the second one is left to the reader as an exercise. We have
Hence
which implies
Many functions involving powers of sine and cosine are hard to integrate. The use of Double-Angle formulas help reduce the degree of difficulty.
Example. Write 
as an expression involving the trigonometric functions with their first power.
Answer. We have
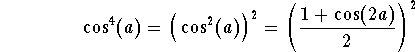
Hence
Since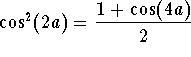 
, we get
or
Example. Verify the identity
Answer.We have
Using the Double-Angle formulas we get
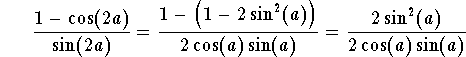
Putting stuff together we get
From the Double-Angle formulas, one may generate easily the Half-Angle formulas
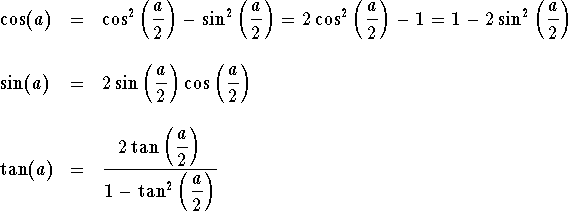
In particular, we have
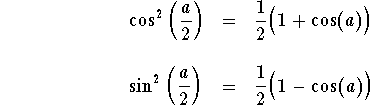
Example. Use the Half-Angle formulas to find
Answer. Set 
. Then
Using the above formulas, we get
Since 
, then 
is a positive number. Therefore, we have
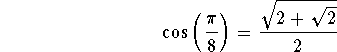
Same arguments lead to
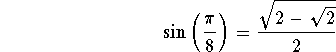
Example. Check the identities
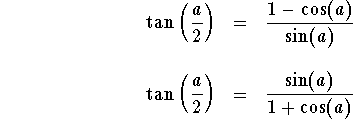
Answer. First note that
which falls from the identity 
. So we need to verify only one identity. For example, let us verify that
using the Half-Angle formulas, we get
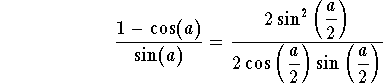
which reduces to
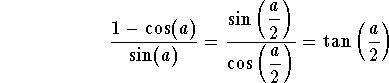
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi