 Operations on Fourier Series
Operations on Fourier Series Operations on Fourier Series
Operations on Fourier Series
The results obtained in this page may easily be extended to function defined on any interval [a,b]. So without loss of generality, we will assume that the functions involved are ![]() -periodic and defined on
-periodic and defined on
![]() .
.
Let f(x) be a ![]() -periodic piecewise continuous function. Then the function
-periodic piecewise continuous function. Then the function
This shows the following:
Theorem. Integration of Fourier series
Let f(x) be ![]() -periodic piecewise continuous function such that a0 = 0. If
-periodic piecewise continuous function such that a0 = 0. If
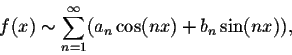
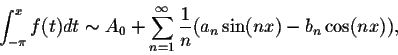
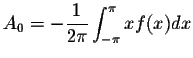 .
.
Since the function F(x) is continuous, we have for any
![]()
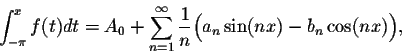
Example. Consider the function
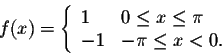
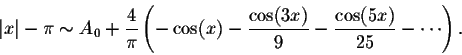
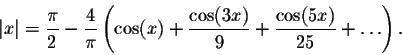
Let f(x) be ![]() -periodic piecewise continuous function such that
-periodic piecewise continuous function such that
![]() .
Set
.
Set
![]() .
Then h(x) is
.
Then h(x) is ![]() -periodic piecewise continuous and satisfies the condition
-periodic piecewise continuous and satisfies the condition
![\begin{displaymath}\int_{x}^{y} f(t)dt = a_0 (y-x) + \sum_{n=1}^{\infty} \int_{x}^{y}\Big[a_n\cos(nt) + b_n \sin(nt)\Big]dt\end{displaymath}](img26.gif)
Theorem. Let f(x) be ![]() -periodic piecewise continuous function. Then for any x and y, the integral
-periodic piecewise continuous function. Then for any x and y, the integral
Example. In the example above, we showed that
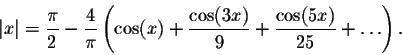
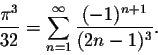
This kind of formulas are quite interesting. Indeed, they enable us to find approximations to the irrational number ![]() .
.
Example. Show that the trigonometric series
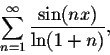
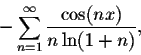
After we discussed the relationship between the Fourier series of a function and its antiderivative, it is natural to ask if a similar relationship exists between a function and its derivative. The answer to this is more complicated. But we do have the following result:
Theoreme. Let f(x) be ![]() -periodic continuous and piecewise smooth function. Then, for any
-periodic continuous and piecewise smooth function. Then, for any
![]() ,
we have
,
we have
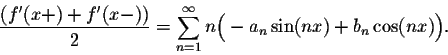
In other words, we obtain the Fourier series of f'(x) by differentiating term-by-term the Fourier series of f(x).
Application: Isoperimetric Inequality
Theoreme. Consider a smooth closed curve in the plane xy. Denote by P its perimeter (total arclength) and by A the area of the region enclosed by the curve. Then we have
Proof. A parametric representation of the curve may be given by
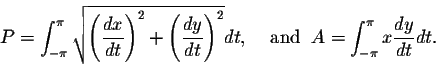
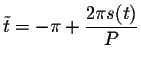 .
If we rewrite the parametric representation in terms of
.
If we rewrite the parametric representation in terms of 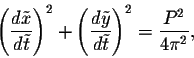
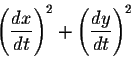
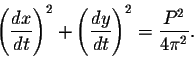
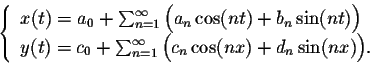
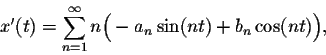
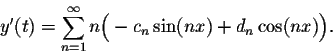
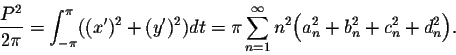
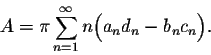
![\begin{displaymath}\frac{P^2}{2\pi} - 2A = \pi \sum_{n=1}^{\infty}
\Big[n(a_n-d...
...+ n(b_n + c_n)^2 + n(n-1)(a_n^2 + b_n^2 + c_n^2 +
d_n^2)\Big].\end{displaymath}](img54.gif)
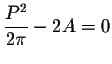 if and only if
if and only if
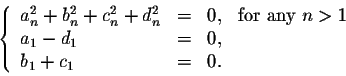
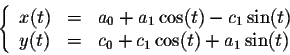
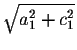 ,
which completes the proof of the theorem.
,
which completes the proof of the theorem.

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi