 Qualitative Analysis
Qualitative Analysis  Qualitative Analysis
Qualitative Analysis

Very often it is almost impossible to find explicitly of implicitly
the solutions of a system (specially nonlinear ones). The qualitative
approach as well as numerical one are important since they allow us to
make conclusions regardless whether we know or not the solutions.
Recall what we did for autonomous equations. First we looked for the
equilibrium points and then, in conjunction with the existence and
uniqueness theorem, we concluded that non-equilibrium solutions are
either increasing or decreasing. This is the result of looking at the
sign of the derivative. So what happened for autonomous systems?
First recall that the components of the velocity vectors are ![]() and
and ![]() . These vectors give
the direction of the motion along the trajectories. We have the four
natural directions (left-down, left-up, right-down, and right-up) and
the other four directions (left, right, up, and down). These
directions are obtained by looking at the signs of
. These vectors give
the direction of the motion along the trajectories. We have the four
natural directions (left-down, left-up, right-down, and right-up) and
the other four directions (left, right, up, and down). These
directions are obtained by looking at the signs of ![]() and
and ![]() and whether they are
equal to 0. If both are zero, then we have an equilibrium point.
and whether they are
equal to 0. If both are zero, then we have an equilibrium point.
Example. Consider the model describing two species competing for the same prey
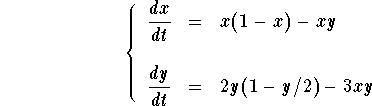
Let us only focus on the first quadrant ![]() and
and ![]() .
First, we look for the equilibrium points. We must have
.
First, we look for the equilibrium points. We must have
![]()
Algebraic manipulations imply
![]()
and
![]()
The equilibrium points are (0,0), (0,2), (1,0), and
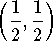 .
.
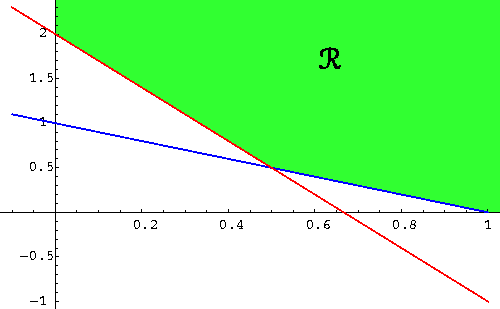
Consider the region R delimited by the x-axis, the y-axis, the line
1-x-y=0, and the line 2-3x-y=0.
|
|
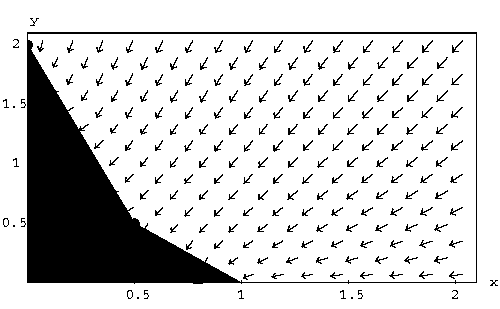
In fact, looking at the first-quadrant, we have three more regions to
add to the above one. The direction of the motion depends on what
region we are in (see the picture below)
|
The boundaries of these regions are very important in determining the
direction of the motion along the trajectories. In fact, it helps to
visualize the trajectories as slope-field did for autonomous
equations. These boundaries are called nullclines.
Nullclines.
Consider the autonomous system
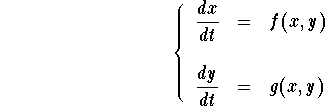
The x-nullcline is the set of points where 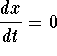 and y-nullcline is the set of points where
and y-nullcline is the set of points where 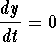 . Clearly the points of intersection between
x-nullcline and y-nullcline are exactly the equilibrium points.
Note that along the x-nullcline the velocity vectors are vertical
while along the y-nullcline the velocity vectors are horizontal. Note
that as long as we are traveling along a nullcline without crossing
an equilibrium point, then the direction of the velocity vector must
be the same. Once we cross an equilibrium point, then we may have a
change in the direction (from up to down, or right to left, and vice-versa).
. Clearly the points of intersection between
x-nullcline and y-nullcline are exactly the equilibrium points.
Note that along the x-nullcline the velocity vectors are vertical
while along the y-nullcline the velocity vectors are horizontal. Note
that as long as we are traveling along a nullcline without crossing
an equilibrium point, then the direction of the velocity vector must
be the same. Once we cross an equilibrium point, then we may have a
change in the direction (from up to down, or right to left, and vice-versa).
Example. Draw the nullclines for the autonomous system and the velocity vectors along them.
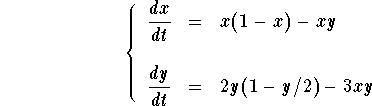
The x-nullcline are given by
![]()
which is equivalent to
![]()
while the y-nullcline are given by
![]()
which is equivalent to
![]()
In order to find the direction of the velocity vectors along the
nullclines, we pick a point on the nullcline and find the direction of
the velocity vector at that point. The velocity vector along the
segment of the nullcline delimited by equilibrium points which
contains the given point will have the same direction. For example,
consider the point (2,0). The velocity vector at this point is
(-1,0). Therefore the velocity vector at any point (x,0), with x
> 1, is horizontal (we are on the y-nullcline) and points to the
left. The picture below gives the nullclines and the velocity vectors
along them.
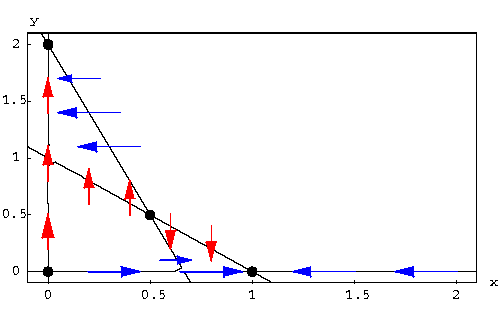
|
In this example, the nullclines are lines. In general we may have any
kind of curves.
Example. Draw the nullclines for the autonomous system
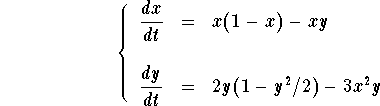
The x-nullcline are given by
![]()
which is equivalent to
![]()
while the y-nullcline are given by
![]()
which is equivalent to
![]()
Hence the y-nullcline is the union of a line with the ellipse
![]()
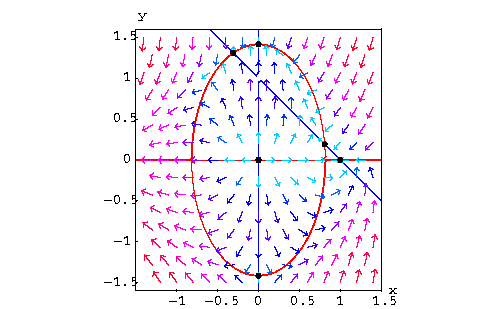
|
Information from the nullclines
For most of the nonlinear autonomous systems, it is impossible to find
explicitly the solutions. We may use numerical techniques to have an
idea about the solutions, but qualitative analysis may be able to
answer some questions with a low cost and faster than the numerical
technique will do. For example, questions related to the long term
behavior of solutions. The nullclines plays a central role in the
qualitative approach. Let us illustrate this on the following
example.
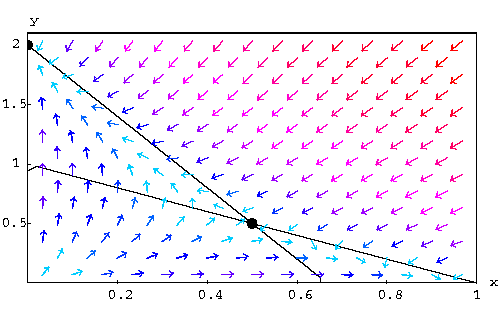
Example. Discuss the behavior of the solutions of the autonomous system
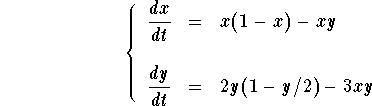
We have already found the nullclines and the direction of the velocity
vectors along these nullclines.

|
These nullclines give the birth to four regions in which the direction of the motion is constant. Let us discuss the region bordered by the x-axis, the y-axis, the line 1-x-y=0, and the line 2-3x-y=0. Then the direction of the motion is left-down. So a moving object starting at a position in this region, will follow a path going left-down. We have three choices
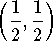 .
.
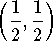 . Then the trajectory will hit
the triangle defined by the points
. Then the trajectory will hit
the triangle defined by the points 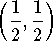 , (0,1), and (0,2). Then it
will go up-left and dies at the equilibrium point (0,2).
, (0,1), and (0,2). Then it
will go up-left and dies at the equilibrium point (0,2).
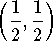 . Then the trajectory will hit
the triangle defined by the points
. Then the trajectory will hit
the triangle defined by the points 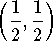 , (1,0), and
, (1,0), and
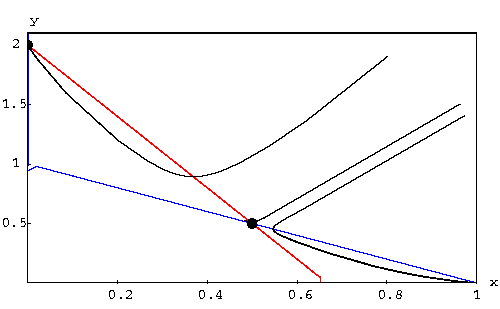
|
For the other regions, look at the picture below. We included some
solutions for every region.
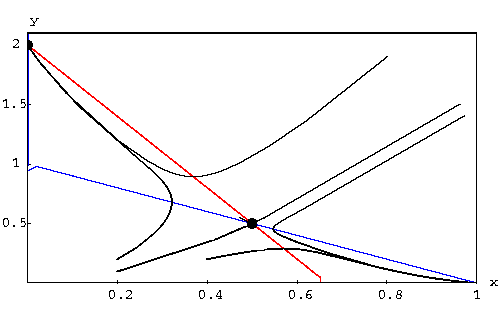
|
Remarks. We see from this example that the trajectories which dye at the
equilibrium point 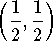 are crucial to predicting the behavior of the solutions. These two
trajectories are called separatrix because they separate the
regions into different subregions with a specific behavior. To find
them is a very difficult problem. Notice also that the equilibrium
points (0,2) and (1,0) behave like sinks. The classification of
equilibrium points will be discussed using the approximation by linear
systems.
are crucial to predicting the behavior of the solutions. These two
trajectories are called separatrix because they separate the
regions into different subregions with a specific behavior. To find
them is a very difficult problem. Notice also that the equilibrium
points (0,2) and (1,0) behave like sinks. The classification of
equilibrium points will be discussed using the approximation by linear
systems.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard..

Author: Mohamed Amine Khamsi