Vector Representations of Solutions
Vector Representations of Solutions
Consider the linear system of differential equations
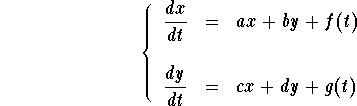
This system may be rewritten using matrix-notation. Indeed, set
,
then the above system is equivalent to the matricial equation
.
Using the matrix product, we get
.
The matrix
is called the coefficient matrix of the system. Note that the coefficients of the matrix A can be constant or not. The vector function
is called the nonhomogeneous term.
Remark: One may think that the equation above is only valid for linear systems of two equations. However, that is not the case. For example, consider the linear system
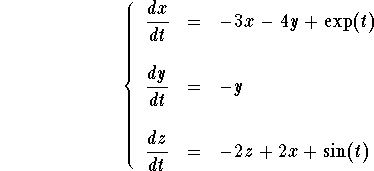
Then, in matricial notation, the system is equivalent to
,
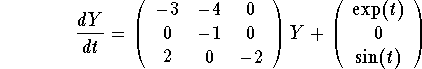where
.
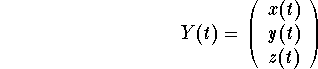Consider the homogeneous linear system
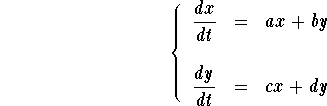
The equilibrium points are given by the equations
Clearly, x=0 and y=0 give a trivial solution. Hence, the function
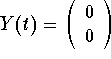gives a constant solution to the linear system. We call it the
trivial solution. In general, the equilibrium points are the
intersection between two lines. Since the two lines intersect,
they are the same (if parallel) or the intersection is reduced to
one point. So, the set of equilibrium points is the entire line
ax+by=0, or the trivial point (0,0). This conclusion is related to
the determinant of the matrix coefficient. Indeed, if
is not equal to 0 (zero), then we have one equilibrium point (the trivial one).
This is may be the most important property for linear systems. Consider the homogeneous linear system
,
then
and 
are two solutions, then 
is also a solution.
This clearly implies that if and are two solutions and 
and 
are two arbitrary constants, then
is also a solution. This conclusion is also known as the Principle of Superposition.
Clearly, from the Principle of Superposition, we may generate plenty
of solutions once two solutions are known. The natural question to
ask therefore, is whether we have obtained all the solutions. In
order to better appreciate this problem let's consider the following example.
Example: Consider the linear system
Show that any solution Y to this system is given as
,
where
and and are two constants.
Answer: It is easy to check that indeed and are solutions to the given system. Let Y be any solution. Set
.
By the uniqueness and existence theorem, Y is the only solution to the IVP
.
Let us find and such that 
. If this is the case, we should have 
, which gives
,
which implies
Clearly, this gives
.
Consider the function
.
The linearity principle implies that 
is a solution. And, since
,
the uniqueness and existence theorem implies that in fact 
gives the desired conclusion.
Remark: When you look at the above example you will notice that what made the conclusion work is that we were able to solve the algebraic system
and this was possible because the two vectors
are linearly independent. In fact, the above conclusion is always valid whenever we have a linear independence around.
and are two solutions to the linear system
.
Assume that the vectors 
and 
are linearly independent. Then, the solution to the IVP
,
is given by
,
for some constants and . In this case, the two-parameter family
,
where and are arbitrary constants, is called the general solution of the system. Then, the two solutions and are said to be linearly independent.
Example: Consider the undamped harmonic oscillator
.
Show that any solution x is given by
.
Answer: Consider the associated linear system
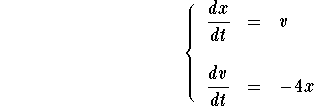
Set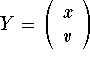 
. Note that the second component is just the derivative of the first one. Consider the two vector functions
It is easy to check that these two vector functions are in fact solutions to the given system. Also, you may check that the two vectors
are linearly independent. Therefore, any solution Y of the system is given by
,
where and are two constants. Using the first component of Y, we see that any solution x(t) of the equation is given by
,
where and are two arbitrary constants.
Clearly, the main problem now is how to find the two linearly independent solutions. This problem will be discussed in the next section and will use the eigenvalue and eigenvector technique.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi