


Throughout these pages I will assume that you are familiar with power series and the concept of the radius of convergence of a power series.
Let us consider the example of the second order differential equation
You probably already know that the solution is given by
![]() ;
recall that this function has as its Taylor series
;
recall that this function has as its Taylor series
Do you remember how to compute the Taylor series expansion for a given function?
If everything works out, then
What does this mean? To compute the Taylor series for the solution to our differential equation, we just have to compute its derivatives. Note that the initial conditions give us a head start: y(0)=1, so a0=1. y'(0)=0, so a1=0.
We can rewrite the differential equation as
Next we differentiate
We can continue in this fashion as long as we like:
Differentiating
We expect that this Taylor polynomial is reasonably close to the solution y(t) of the differential equation, at least close to t=0. In the picture below, the solution
![]() is drawn in red, while the power series approximation
is drawn in red, while the power series approximation
![]() is depicted in blue:
is depicted in blue:
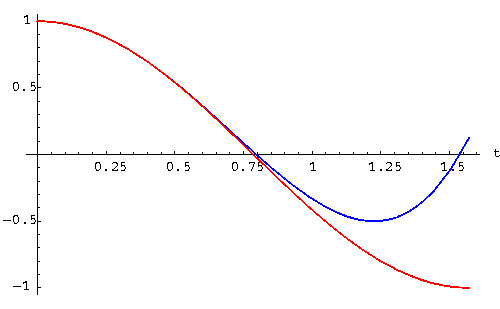
|
The method outlined works also in theory for non-linear differential equations, even though the computational effort usually becomes prohibitive after the first few steps. Let's consider the example
Next we differentiate
Let's continue a little bit longer: We differentiate
Differentiating
The fifth degree Taylor polynomial approximation to the solution of our differential equation has the form
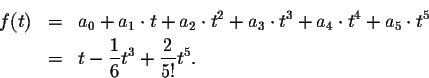
We again expect that this Taylor polynomial is reasonably close to the solution y(t) of the differential equation, at least close to t=0. In the picture below, the solution, as computed by a numerical method, is drawn in red, while the power series approximation
![]() is depicted in blue:
is depicted in blue:
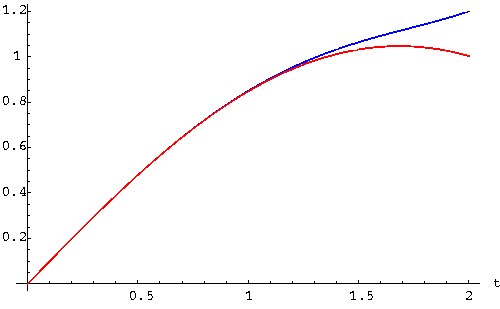
|
The next sections will develop an organized method to find power series solutions for second order linear differential equations. Here are a couple of examples to practice what you have learned so far:

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust