 Integrating Factor Technique
Integrating Factor Technique  Integrating Factor Technique
Integrating Factor Technique

Assume that the equation
![]() ,
,
is not exact, that is-
![]()
In this case we look for a function u(x,y) which makes the new equation
![]() ,
,
an exact one. The function u(x,y) (if it exists) is called the integrating factor. Note that u(x,y) satisfies the following equation:
![]()
This is not an ordinary differential equation since it involves more than one variable. This is what's called a partial differential equation. These types of equations are very difficult to solve, which explains why the determination of the integrating factor is extremely difficult except for the following two special cases:
![]() ,
,
is a function of x only, that is, the variable y disappears from the expression. In this case, the function u is given by
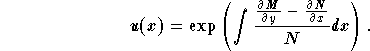
![]() ,
,
is a function of y only, that is, the variable x disappears from the expression. In this case, the function u is given by
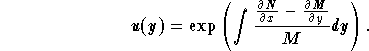
Let us summarize the above technique. Consider the equation
![]()
If your equation is not given in this form you should rewrite it first.
![]() ,
,
then compare them.
![]()
If this expression is a function of x only, then go to step 3. Otherwise, evaluate
![]()
If this expression is a function of y only, then go to step 3.
Otherwise, you can not solve the equation using the technique
developped above!
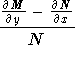 is a function of
x only. Then an
integrating factor is given by
is a function of
x only. Then an
integrating factor is given by 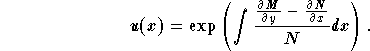 ;
;
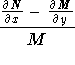 is a function of
y only, then an
integrating factor is given by
is a function of
y only, then an
integrating factor is given by
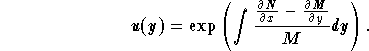
The following example illustrates the use of the integrating factor technique:

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi