 Population Dynamics
Population Dynamics

Here are some natural questions related to population problems:
- What will the population of a certain country be in ten years?
- How are we protecting the resources from extinction?
More can be said about the problem but, in this little review we will
not discuss them
in detail. In order to illustrate the use of
differential equations with regard to this problem we consider the
easiest mathematical model offered to govern the population dynamics
of a certain species. It is commonly called the exponential
model, that is, the rate of change of the population is proportional
to the existing population. In other words, if P(t) measures the population,
we have
 ,
,
where the rate k is constant. It is fairly easy to see that if k >
0, we have growth, and if k <0, we have decay. This is a
linear equation which solves into
 ,
,
where 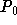 is the initial population, i.e.
is the initial population, i.e. 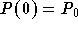 . Therefore,
we conclude the following:
. Therefore,
we conclude the following:
- if k>0, then the population grows and continues to expand to
infinity, that is,

- if k<0, then the population will shrink and tend to 0. In
other words we are facing extinction.
Clearly, the first case, k>0, is not adequate and the model can be
dropped. The main argument for this has to do with environmental
limitations. The complication is that population growth is eventually
limited by some factor, usually one from among many essential
resources. When a population is far from its limits of growth it can
grow exponentially. However, when nearing its limits the population
size can fluctuate, even chaotically. Another model was proposed to
remedy this flaw in the exponential model. It is called the
logistic model (also called Verhulst-Pearl model). The
differential equation for this model is
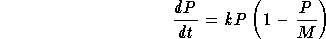 ,
,
where M is a limiting size for the population (also called the
carrying capacity). Clearly, when P is small compared to M,
the equation reduces to the exponential one. In order to solve
this equation we recognize a nonlinear equation which is separable. The
constant solutions are P=0 and P=M. The non-constant solutions
may obtained by separating the variables
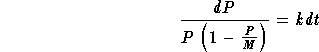 ,
,
and integration
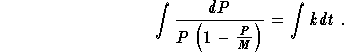
The partial fraction techniques gives
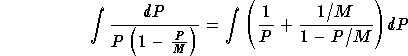 ,
,
which gives
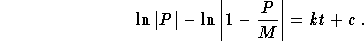
Easy algebraic manipulations give
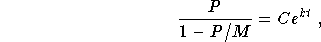
where C is a constant. Solving for P, we get

If we consider the initial condition 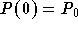 (assuming that
(assuming that 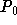 is not equal to both 0 or M), we get
is not equal to both 0 or M), we get
 ,
,
which, once substituted into the expression for P(t) and simplified,
we find
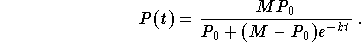
It is easy to see that

However, this is still not satisfactory because this model does not tell us when
a population is facing extinction since it never implies that. Even
starting with a small population it will always tend to the carrying
capacity M.
If you would like more practice, click on
Example.

[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Mohamed
Amine Khamsi
Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Population Dynamics
Population Dynamics  Population Dynamics
Population Dynamics 
![]() ,
, ![]() ,
, ![]() is the initial population, i.e.
is the initial population, i.e. ![]() . Therefore,
we conclude the following:
. Therefore,
we conclude the following:
![]()
![]() ,
, 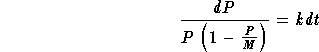 ,
, 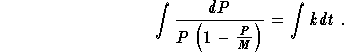
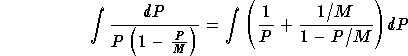 ,
, ![]()
![]()
![]()
![]() (assuming that
(assuming that ![]() is not equal to both 0 or M), we get
is not equal to both 0 or M), we get
![]() ,
, ![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 