Conditional Convergence

We have seen that, in general, for a given series , the series may not be convergent. In other words, the series is not absolutely convergent. So, in this case, it is almost a lost case, meaning it is very hard to use the old tools developed for positive series. But, for a very special kind of series we do have a partial answer (due to Abel). This is the case for alternating series. These are of the form

,

where .

Example: The series

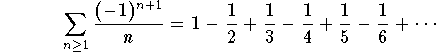
is alternating. Note that we do not have , but . This is not important. What matters is that the sign alternates; once it is positive, the next one is negative and so on....

Main Problem: When does an alternating series converge?

In order to appreciate Abel's result on alternating series, let us play with the above example. Indeed, consider the series

.

Let us generate the sequence of partial sums . We have

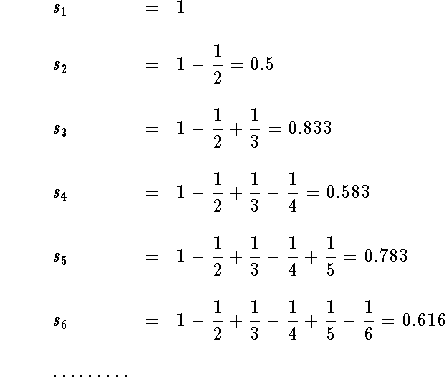
This clearly implies

.

So, one may wonder whether the even sequence is increasing and the odd sequence is decreasing while satisfying

.

The answer is: YES. Indeed, we have

,

which implies . Let us check that is increasing (the odd one is left to the reader to prove). We have

.

Since

,

then we have , which implies that is increasing. By the way, we did evaluate 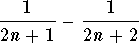, but, in fact, we did not need that. What makes it work is the fact that the sequence is decreasing. So, since the sequence is increasing and bounded above by , then it is convergent to a number A. The same holds for which is decreasing and bounded below by . Hence, it is convergent to a number B. We must have

.

This obviously implies

.

Since

,

we deduce that we must have A = B, which gives

.

This clearly implies that the sequence is convergent and

.

Therefore, the series

is convergent and we have

.

From the above inequalities, we get

,

for any . These inequalities allow for an approximation of the total sum by the partial sums. If you wonder what the total sum is, the answer is (by using Taylor series):

.

Remark: Let us give another way to prove

.

First, consider the sequence defined by

.

It is easy to check that , for . Let us show that is decreasing. Indeed, we have

.

Set

.

We have

.

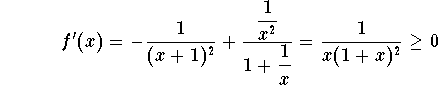Hence, the function f(x) is increasing for . Since

,

then we must have for . This implies

ln$$\left(\vphantom{1 + \frac{1}{x} }\right.$$1 + $${\frac{{1}}{{x}}}$$$$\left.\vphantom{1 + \frac{1}{x} }\right)$$ $$\geq$$ $${\frac{{1}}{{x+1}}}$$

for . Hence, we have

ln$$\left(\vphantom{\frac{n+1}{n} }\right.$$$${\frac{{n+1}}{{n}}}$$$$\left.\vphantom{\frac{n+1}{n} }\right)$$ $$\geq$$ $${\frac{{1}}{{n+1}}}$$

for . Therefore, the sequence is decreasing. Since it is bounded below by 0, we conclude that is convergent. Write

.

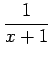
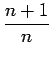
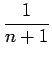
C is called Euler's constant. We have

,

for any . Let us go back to the alternating series

.

We have

.

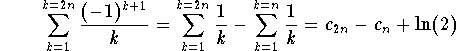Since

,

we conclude that

.

So what did we learn from the above example? By looking carefully at the above calculations, we may be able to come up with a more general result.

Alternating Series Test:

Consider the alternating series

where . Assume that:

1.

is decreasing;

2.

;

Then the series

is convergent. Moreover, the estimate of the total sum

,

by the nth partial sum , has error of magnitude at most. In other words, we have

.

Example: Classify the series

as either absolutely convergent, conditionally convergent, or divergent.

Answer: Consider the series of the absolute values

.

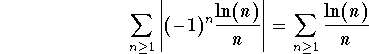This is a Bertrand Series with and . Using the Bertrand Series Test, we conclude that it is divergent. Hence, the series

is not absolutely convergent. Since this series is alternating, with

,

let us check if the assumptions of the Alternating Series Test are satisfied. First, we need to check that is decreasing. Set

.

We have

.

Clearly, we have f '(x) < 0, for x > e. Hence, the sequence 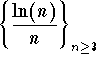is decreasing. It is easy to check that

.

Therefore, all the Alternating Series Test assumptions are satisfied. We then conclude that the series

is convergent. In fact, in order to be precise it is conditionally convergent.

Example: Classify the series

as either absolutely convergent, conditionally convergent, or divergent.

Answer: It is not clear from the definition what this series is. So we advise you to take your calculator and compute the first terms to check that in fact we have

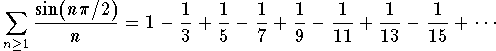
This is the case because

So, this is an alternating series with 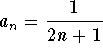. Since this sequence is decreasing and goes to 0 as , then by the Alternating Series Test, the series

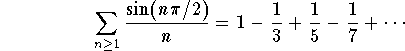
is convergent. Note that it is not absolutely convergent.

[Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour