More Challenging Limits

We have seen in previous pages some fundamental examples that you should know. Here we will discuss some challenging examples. We advise you to first try to find the solution before you read the answer. Good Luck...

Example: For any real number a, define [a] to be the largest integer less than or equal to a. Let x be a real number. Show that the sequence where

is convergent. Find its limit.

Answer: For any real number a, we have

,

or

.

Hence, for any integer , we have

.

This implies

,

which is the same as

.

Since

,

we get

.

Dividing by , we get

.

Since

,

the Pinching Theorem gives

.

Example: Let be a convergent sequence. Show that the new sequence

is convergent. Moreover, we have

.

Answer: Set

.

Algebraic manipulation give

.

Let . Then, there exists , such that for any , we have

.

Hence, for , we have

,

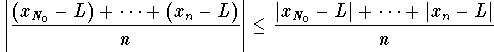which implies

.

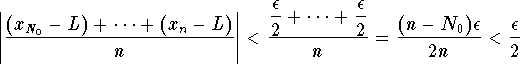Write

.

Since , then there exists such that for any , we have

.

Putting these equations together, we get

.

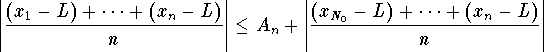So, for , we get

.

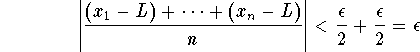This completes the proof of our statement.

Remark: The new sequence generated from is called the Cesaro Mean of the sequence. Note that for the sequence the Cesaro Mean converges to 0, while the initial sequence does not converge.

In the next example we consider the Geometric Mean.

Example: Let be a sequence of positive numbers (that is for any ). Define the geometric mean by

.

Show that if is convergent, then is also convergent and

.

Answer: Since , we may use the logarithmic function to get

.

This means that the sequence is the Cesaro Mean of the sequence . Since is convergent, we deduce that is also convergent. Moreover, we have

.

Using the previous example we conclude that the sequence is convergent and

,

using the exponential function, we deduce that the sequence is convergent and

.

Example: Let be a sequence of real numbers such that

.

Show that

.

Answer: Write . Then, we have

$$x_n - x_1 = (x_n - x_{n-1}) + \cdots+ (x_3 - x_2) + (x_2 - x_1) = v_{n-1} + \cdots + v_2 + v_1 \;.$$

In other words, the sequence is the Cesaro Mean of the sequence . Since

,

the sequence is also convergent. Moreover, we have

.

Remark: A similar result for the ratio goes as follows:

Let be a sequence of positive numbers (that is, for any ). Assume that

.

Show that

.

Answer:

Below are some more challenging examples. Click on Answer, to get some hints on the solution.

Problem 1: Let be a sequence of positive numbers (that is, for any ). Assume that

.

Show that

1.

If |L| <1, then

2.

If |L| > 1, then the sequence is not convergent.

3.

What can be said about when |L| = 1?

4.

Use the above to discuss convergence of

where x is any real number.

Answer:

Problem 2: Define the sequence by

.

1.

Show that for any , we have

.

2.

Show that is decreasing.

3.

Deduce from 1. and 2. that is convergent and find its limit.

Answer:

[Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour