The Ratio Test
The Ratio TestThis problem is slightly trickier. If you have trouble finding the general term of the series, try the following: Ask, what happens as you move from one term to the next:
Upstairs we multiply by 2 and by x, downstairs we multiply by 3 and replace n by n+1 (this really means we multiply the term by n and divide by n+1). Thus the absolute ratio will be given by
More formally, the general term of the series has the form
leading to the same absolute ratio:
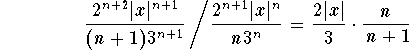
Thus the limit of the absolute ratios is given by:
The series will converge as long as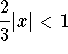 
(the series will diverge when 
).
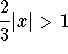Consequently, the radius of convergence equals 
;
the series will converge in an interval from 
to .
It is actually easier to find the radius of convergence when one uses the summation notation for the series. The general term is then already given!
. Here is a massive hint: Do you remember that
