 The Bisection Method
The Bisection Method
 The Bisection Method
The Bisection Method
The Bisection Method at the same time gives a proof of the Intermediate Value Theorem and provides a practical method to find roots of equations. If your calculator can solve equations numerically, it most likely uses a combination of the Bisection Method and the Newton-Raphson Method.
Recall the statement of the Intermediate Value Theorem: Let
f (x) be a continuous function on the interval [a, b]. If
d ![]() [f (a), f (b)], then there is a
c
[f (a), f (b)], then there is a
c ![]() [a, b] such that
f (c) = d.
[a, b] such that
f (c) = d.
By replacing f (x) by f (x) - d, we may assume that d = 0; it
then suffices to obtain the following version: Let f (x) be a
continuous function on the interval [a, b]. If f (a) and f (b)
have opposite signs, then there is a
c ![]() [a, b] such that
f (c) = 0.
[a, b] such that
f (c) = 0.
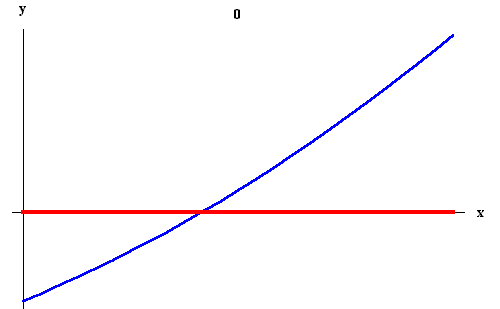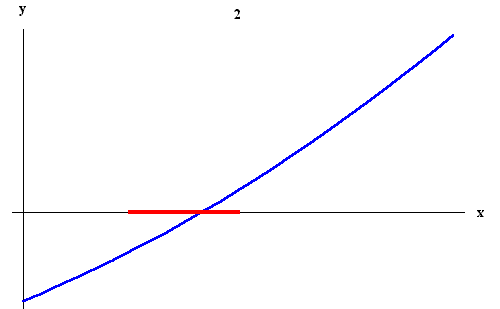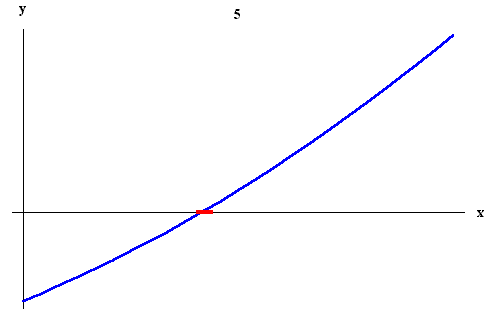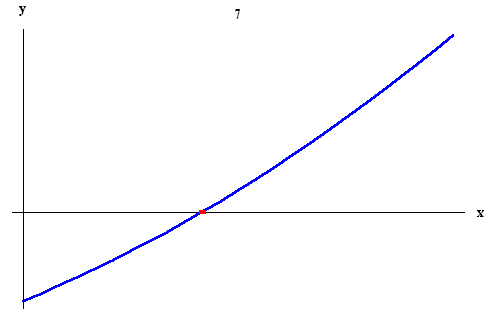
Here is an outline of its proof: Let's assume that f (a) < 0, while f (b) > 0, the other case being handled similarly. Set a0 = a and b0 = b.
Now consider the midpoint
m0 = 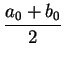 ,
and evaluate f (m0). If f (m0) < 0, set a1 = m0 and b1 = b0.
If f (m0) > 0, set a1 = a0 and b1 = m0. (If f (m0)=0, you're
already done.) What situation are we in now? f (a1) and
f (b1) still have opposite signs, but the length of the interval
[a1, b1] is only half of the length of the original interval
[a0, b0]. Note also that
a0
,
and evaluate f (m0). If f (m0) < 0, set a1 = m0 and b1 = b0.
If f (m0) > 0, set a1 = a0 and b1 = m0. (If f (m0)=0, you're
already done.) What situation are we in now? f (a1) and
f (b1) still have opposite signs, but the length of the interval
[a1, b1] is only half of the length of the original interval
[a0, b0]. Note also that
a0 ![]() a1 and that
b0
a1 and that
b0 ![]() b1.
b1.
You probably guess this by now: we will do this procedure again and again.
Here is the second step: Consider the midpoint
m1 = 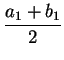 , and evaluate f (m1). If f (m1) < 0, set
a2 = m1 and b2 = b1. If f (m1) > 0, set a2 = a1 and
b2 = m1. (If f (m1)=0, you're already done.) What situation
are we in now? f (a2) and f (b2) still have opposite signs,
but the length of the interval [a2, b2] is only a quarter of
the length of the original interval [a0, b0]. Note also that
a0
, and evaluate f (m1). If f (m1) < 0, set
a2 = m1 and b2 = b1. If f (m1) > 0, set a2 = a1 and
b2 = m1. (If f (m1)=0, you're already done.) What situation
are we in now? f (a2) and f (b2) still have opposite signs,
but the length of the interval [a2, b2] is only a quarter of
the length of the original interval [a0, b0]. Note also that
a0 ![]() a1
a1 ![]() a2 and that
b0
a2 and that
b0 ![]() b1
b1 ![]() b2.
b2.
 |
Continuing in this fashion we construct by induction two sequences
It follows from the first two properties that the sequences (an) and (bn) converge; set
The crucial observation is the fact that the fourth property implies that a = b. Consequently, f (a) = f (b) = 0, and we are done.
Example. Let's compute numerical approximations for the
![]() with the help of the bisection method. We set
f (x) = x2 - 2. Let us start with an interval of length one: a0 = 1
and b1 = 2. Note that
f (a0) = f (1) = - 1 < 0, and
f (b0) = f (2) = 2 > 0.
Here are the first 20 applications of the bisection algorithm:
with the help of the bisection method. We set
f (x) = x2 - 2. Let us start with an interval of length one: a0 = 1
and b1 = 2. Note that
f (a0) = f (1) = - 1 < 0, and
f (b0) = f (2) = 2 > 0.
Here are the first 20 applications of the bisection algorithm:
 |
A comparison of the Bisection Method and the Newton-Raphson Method. The Newton-Raphson Method is often much faster than the Bisection Method. In the last example, we started with an interval of length 1. After 10 steps, the interval [a10, b10] has length 1/1024. Consequently every 10 steps of the Bisection Method will give us about 3 digits more accuracy - that is rather slow. (On the Newton-Raphson Method page, we did the same example, compare the speeds of convergence!)
The Newton-Raphson Method can be unreliable: If the algorithm encounters a point x where f '(x) = 0, it crashes; if it encounters points where the derivative is very close to 0, it will become very unreliable.
The Bisection Method on the other hand will always work, once you have found starting points a and b where the function takes opposite signs.
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi