 SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS SOLVING TRIGONOMETRIC EQUATIONS
SOLVING TRIGONOMETRIC EQUATIONS
Note:
If you would like an review of trigonometry, click on trigonometry.
Solve for x in the following equation.
Example 1:
There are an infinite number of solutions to this problem. To solve for x,
you must first isolate the sine term.
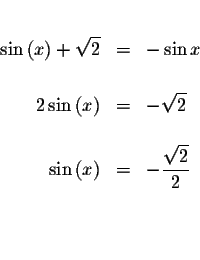
If we restriction the domain of the sine function to
![$\left[ -\displaystyle \frac{\pi }{2}
\leq x\leq ,\displaystyle \frac{\pi }{2}\right] $](img3.gif) ,
we can use the inverse sine function
to solve for reference angle x, and then x.
,
we can use the inverse sine function
to solve for reference angle x, and then x.
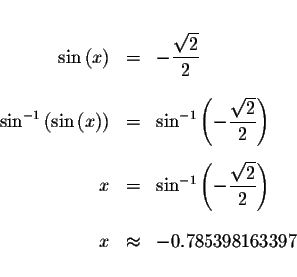
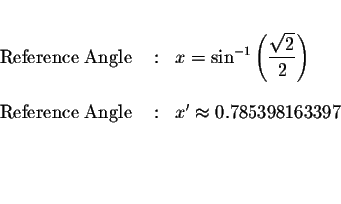
We know that the ![]() e function is negative in the third and the fourth
quadrant. Therefore two of the solutions are the angle
e function is negative in the third and the fourth
quadrant. Therefore two of the solutions are the angle
![]() that terminates in the third quadrant and the angle
that terminates in the third quadrant and the angle
![]() that
terminates in the fourth. We have already solved for
that
terminates in the fourth. We have already solved for
![]()
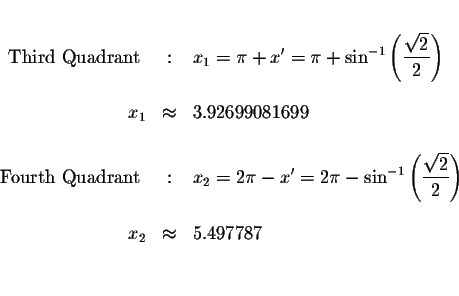
The solutions are
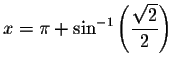 and
and
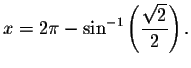
The period of the sin
![]() function is
function is ![]() This means that
the values will repeat every
This means that
the values will repeat every ![]() radians in both directions. Therefore,
the exact solutions are
radians in both directions. Therefore,
the exact solutions are
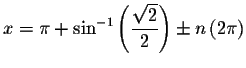 and
and
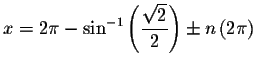 where n is an integer.
where n is an integer.
The approximate solutions are
![]() and
and
![]() where n is an
integer.
where n is an
integer.
These solutions may or may not be the answers to the original problem. You much check them, either numerically or graphically, with the original equation.
Numerical Check:
Check answer x=3.92699081699
Since the left side equals the right side when you substitute 3.92699081699for x, then 3.92699081699 is a solution.
Check answer
x=5.497787
Since the left side equals the right side when you substitute 5.497787 for x, then 5.497787 is a solution.
Graphical Check:
Graph the equation
Note that the graph crosses the x-axis many times indicating many solutions.
Note that it crosses at
3.92699081699. Since the period is
![]() ,
it crosses again at
3.92699081699+6.2831853=10.21017 and at
3.92699081699+2(6.2831853)=16.49336, etc.
,
it crosses again at
3.92699081699+6.2831853=10.21017 and at
3.92699081699+2(6.2831853)=16.49336, etc.
The graph also crosses the x-axis at 5.497787. Since the period is
![]() ,
it crosses again at
5.497787+6.2831853=11.78097 and at
5.497787+2(6.2831853)=18.06415, etc.
,
it crosses again at
5.497787+6.2831853=11.78097 and at
5.497787+2(6.2831853)=18.06415, etc.
If you would like to test yourself by working some problems similar to this example, click on Problem.
If you would like to go back to the equation table of contents, click on Contents.
This site was built to accommodate the needs of students. The topics and problems are what students ask for. We ask students to help in the editing so that future viewers will access a cleaner site. If you feel that some of the material in this section is ambiguous or needs more clarification, please let us know by e-mail.

