 Sign of a Quadratic Function with Application to Inequalities
Sign of a Quadratic Function with Application to Inequalities  Sign of a Quadratic Function with Application to Inequalities
Sign of a Quadratic Function with Application to Inequalities

Many inequalities lead to finding the sign of a quadratic expression. let us discuss this problem here. Consider the quadratic function
![]()
We know that
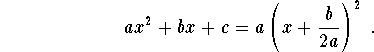
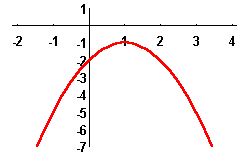
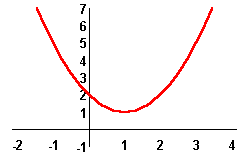
In this case, the function ![]() has the sign of the coefficient a.
has the sign of the coefficient a.
| |
|
| 
|
![]()
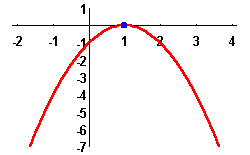
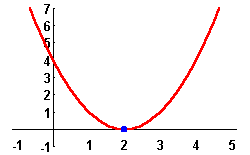
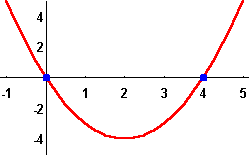
where ![]() and
and ![]() are the two roots with
are the two roots with ![]() . Since
. Since ![]() is always positive when
is always positive when ![]() and
and ![]() , and always negative when
, and always negative when ![]() , we get
, we get
| |
|
| 
|
| |
|
| 
|
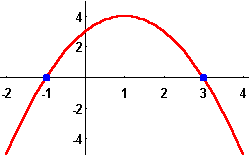
Example: Solve the inequality
![]()
Solution. First let us find the root of the quadratic equation ![]() . The quadratic formula gives
. The quadratic formula gives
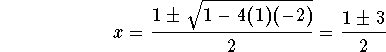
which yields x= -1 or x=2. Therefore, the expression
![]() is negative or equal to 0 when
is negative or equal to 0 when ![]() .
.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi