Solutions or Roots of Quadratic Equations
Solutions or Roots of Quadratic Equations
Consider the quadratic equation
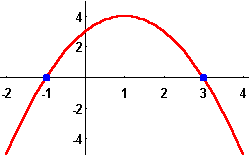
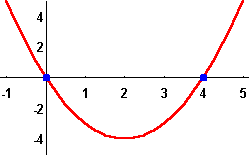
A real number x will be called a solution or a root if it satisfies the equation, meaning 
. It is easy to see that the roots are exactly the x-intercepts of the quadratic function 
, that is the intersection between the graph of the quadratic function with the x-axis.
| |
|
| 
|
Example 1: Find the roots of the equation
Solution. This equation is equivalent to
Since 1 has two square-roots 
, the solutions for this equation are
Example 2: Find the roots of the equation
Solution. This example is somehow trickier than the previous one but we will see how to work it out in the general case. First note that we have
Therefore the equation is equivalent to
which is the same as
Since 3 has two square-roots 
, we get
which give the solutions to the equation
We may then wonder whether any quadratic equation may be reduced to the simplest ones described in the previous examples. The answer is somehow more complicated but it was known for a very longtime (to the Babylonians about 2000 B.C. ). Their idea was based mainly on completing the square which we did in solving the second example.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi