 The Method of Partial Fractions
The Method of Partial Fractions The Method of Partial Fractions
The Method of Partial Fractions
Early in Algebra you learn how to combine "simple'' fractions into a "more complicated'' one. Here is a typical example:
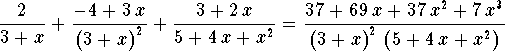
The Method of Partial Fractions does the opposite: It dissects a complicated fraction into a sum of simple fractions. While this is a little more complicated than going the other direction, it is also more useful. Major applications of the method of partial fractions include:
A simple fraction is a fraction with a simple denominator. The first step consists of detecting the factors (the building blocks) of the given denominator. The Fundamental Theorem of Algebra tells us what is possible: Every polynomial can be factored into linear factors (degree 1 polynomials) and irreducible polynomials of degree 2.
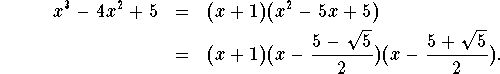
![]()
![]()
There are different methods to decide:
 |
 |
| |
![]()
Since the discriminant (the expression under the radical) is negative, the polynomial is irreducible!