PROPERTIES OF LOGARITHMS

SOLVING LOGARITHMIC EQUATIONS

1. To solve a logarithmic equation, rewrite the equation in exponential form and solve for the variable.

Example 5: Consider the function

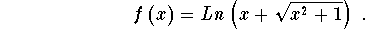
Find the inverse .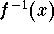

Solution:

Step 1: From the graph, we determine that the function f(x) is one-to-one and therefore has a unique inverse. How can you tell from the graph that a function is one-to-one? Use the horizontal line test. Mentally run a horizontal line over the graph. If at any time, the line touches the graph in more than one place, it is not a one-to-one function.

Step 2: Since f(x) is a one-to-one function, we know that the inverse exists. The inverse of a logarithmic function is an exponential function.

Step 3: We know that the domain and range of f(x) are equal to the range and domain of 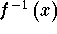. From the graph of f(x), the domain is the set of all real numbers, and the range is the set of all positive real numbers.

Step 4: We know that the composition of a function with its inverse will yield x or

Step 5: Find f(inverse):

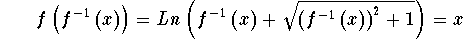
Step 6: Convert the equation to an exponential equation:

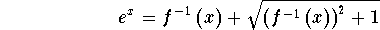
Step 7: Isolate the 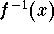term using steps 8 through 13.

Step 8: Subtract 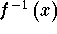from both sides of the above equation:

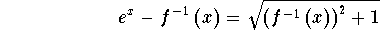
Step 9: Square both sides of the above equation:

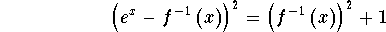
Step 10: Expand the left side of the above equation:

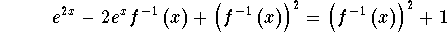
Step 11: Subtract 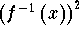from both sides of the above equation:

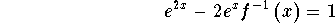
Step 12: Subtract 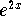from both sides of the above equation:

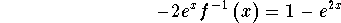
Step 13: Divide both sides of the above equation by 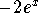to get

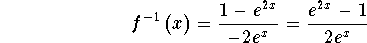
Check: You can check the problem by graphing the function f(x), graphing its inverse, and graphing the line y = x. If the graphs of the function and its inverse are symmetric to the line y = x, you have correctly found the inverse.
You can also check your answer by finding a point on the original graph, say (a, b), and determine whether the point (b,a) is on the graph of the inverse. This is not a perfect check, but it will alert you of a wrong answer.
For example,

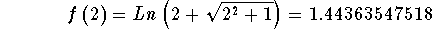
indicates that the point 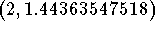is a point on the graph of f(x).

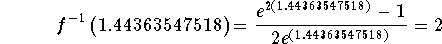
indicates that the point 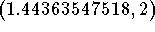is located on the graph of .

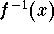If you would like to review another example, click on Example.

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.