RULES OF LOGARITHMS -Example

Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.

Logarithmic Rule 3: .

Example 6: Rewrite the term 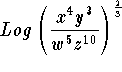tex2html_wrap_inline242 as the sum and difference of fully simplified terms.

Solution:

Step 1: The first thing that you should note is that we are taking the log of an expression raised to the power

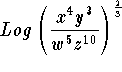. We can simplify this by using Rule 3: tex2html_wrap_inline242

can be written tex2html_wrap_inline248

Step 2: The second thing that you should note is that you now have the log of a quotient. We can simplify this by using Rule 2: tex2html_wrap_inline248

can be written

Step 3: The third thing that you should note is that you now have logs of products. We can simplify this by using Rule 1: tex2html_wrap_inline254

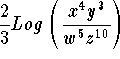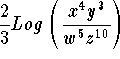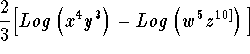can be written as

Step 4: The fourth thing that you should note is that you now have the logs of expressions raised to powers

can be written

Step 5: The fifth thing that you should note is that you can simplify this by multiplying each of the terms by

can be written

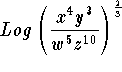Comment: We have stated that tex2html_wrap_inline242

is equivalent to

Is this true always? No, it is only true for certain values of x, y, w, and z.. Remember that you cannot take the log of any number less than or equal to 0. In the initial expression, we need to find values of x, y, w, and w so that 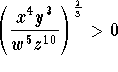tex2html_wrap_inline272 . There are many combinations. In one case the y and the w could be negative. In the final expression, we need to find values of x, y, w, and z so that

can be calculated. In this case x, y, w, and z must all be greater than 0. You use the domain that is common to both expressions. Therefore, x, y, w, and z must all be greater than 0.

How could you check your answer? The initial expression and each subsequent expression are equivalent. This means that if we pick any positive numbers for x, y, w, and z and substitute them in each of the expressions, the values will be the same. Let's do it for x = 2, y = 3, w = 4, and z = 5.

Original Expression: The value of 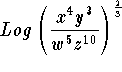tex2html_wrap_inline242 when we substitute the values for x, y, w, and z is

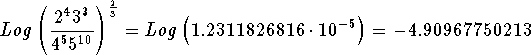
displaymath278

Step 1 Expression: The value of 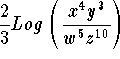tex2html_wrap_inline248 when we substitute the values for x, y, w, and z is

displaymath282

Step 2 Expression: The value of 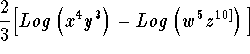tex2html_wrap_inline254 when we substitute the values for x, y, w, and z is

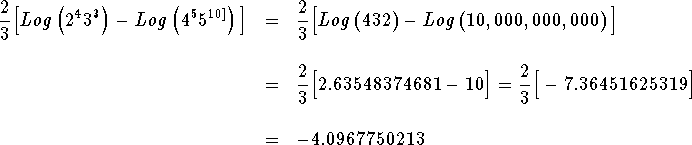
displaymath286

Step 3 Expression: The value of

when we substitute the values for x, y, w, and z is

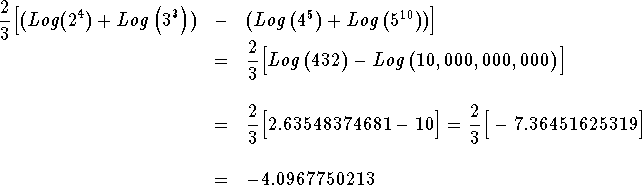
displaymath290

Final Expression: The value of

when we substitute the values for x, y, w, and z is

We have illustrated our answer.

If you would like to review another example, click on Example.

[Previous Example] [Next Example] [Menu Back to Rule 3]

[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus