RULES OF LOGARITHMS - Example

Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.

Logarithmic Rule 2:

Example 5: Expand 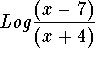and state the domain.

Solution: The domain of 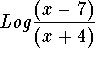is the set of all real numbers such that

Either x-7>0 and x+4>0 or x-7<0 and x+4<0 .
This means that if x > 7 and x > - 4, both the numerator and the denominators are positive and the value of the fraction is positive. If we restrict the values of x to be greater than 7, they are automatically greater than - 4 and the domain can be simplified to x > 7.

or

This means that if x > 7 and x < -4, both the numerator and the denominator are negative, and the value of the fraction is positive. If we restrict the values of x to be less than - 4, they are automatically less than 7, and the domain can be simplified to x < -4.

The domain of 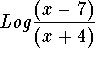is the set of all real numbers that are in the interval or , that is

The domain of is the set of real numbers that works for both. The real number x > 7 works for the first term and the real number x > -4 works for the second term. You need a set of numbers that will work for both terms. The domain is the set of real numbers where x > 7.

Therefore, 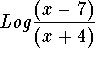is equivalent to only when the domain is restricted to those real numbers x > 7.

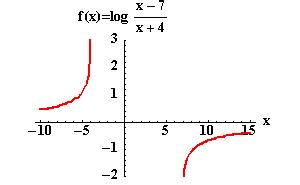
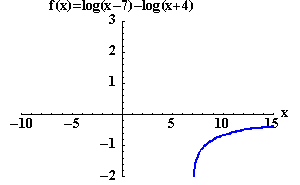
If you would like to review another example, click on Example.

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.