 A REVIEW OF LOGARITHMS
A REVIEW OF LOGARITHMS
 A REVIEW OF LOGARITHMS
A REVIEW OF LOGARITHMS
Many students in high school and in college have a difficult time with logarithms. In many cases, they memorize the rules without fully understanding them, and they sometimes even manage to squeak by a course. Why waste their time on these archaic entities; they are never going to see them again. Wrong! Just when the student breathes a sigh of relief to be done with logarithms, they encounter them again in another course. They are now in trouble because the second encounter with logarithms is at a more sophisticated level. Without an understanding of the basics, the student is doomed to blindly stumble through and fail the course. You have our sympathy and you have our solution. We at S.O.S. Math want you to succeed. We have prepared a review of logarithms for you with examples and problems. You can start at the beginning or jump in at any place.
Since logarithms are exponents, we will review exponential functions before we review logarithms and logarithmic functions. Before we review exponential functions, we will present a brief history of logarithms and a brief discussion of the functions.
History of Logarithms:
Logarithms were invented independently by John Napier, a Scotsman, and by Joost Burgi, a Swiss. The logarithms which they invented differed from each other and from the common and natural logarithms now in use. Napier's logarithms were published in 1614; Burgi's logarithms were published in 1620. The objective of both men was to simplify mathematical calculations. Napier's approach was algebraic and Burgi's approach was geometric. Neither men had a concept of a logarithmic base. Napier defined logarithms as a ratio of two distances in a geometric form, as opposed to the current definition of logarithms as exponents. The possibility of defining logarithms as exponents was recognized by John Wallis in 1685 and by Johann Bernoulli in 1694.
The invention of the common system of logarithms is due to the combined effort of Napier and Henry Briggs in 1624. Natural logarithms first arose as more or less accidental variations of Napier's original logarithms. Their real significance was not recognized until later. The earliest natural logarithms occur in 1618.
Logarithms are useful in many fields from finance to astronomy.
Shortcuts
Multiplication is a shortcut for addition.
Recall that ![]() means 5 + 5+ 5.
Exponents are a
shortcut for multiplication. Recall that
means 5 + 5+ 5.
Exponents are a
shortcut for multiplication. Recall that ![]() means
means ![]() .
Logarithm is a shortcut for exponents.
.
Logarithm is a shortcut for exponents.
Function
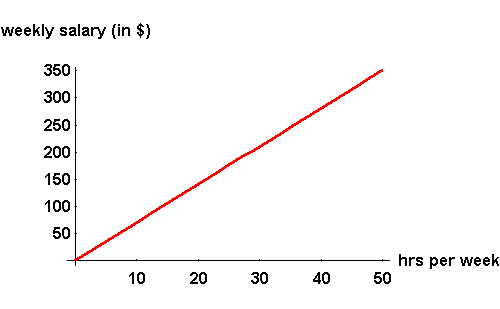
Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second number in an orderly and specific manner. All the points on the graph of a function are made up of two parts: (a number, and the function value at that number). For example, the number of hours worked in a week could be the first number, and the salary for the week could be the function value. If an hourly salary is $7.00, then the rule would be 7 times the number of hours worked.
|
You could identify a point on the graph of a function as (x,y) or (x, f(x)). You may have only one function value for each x number.
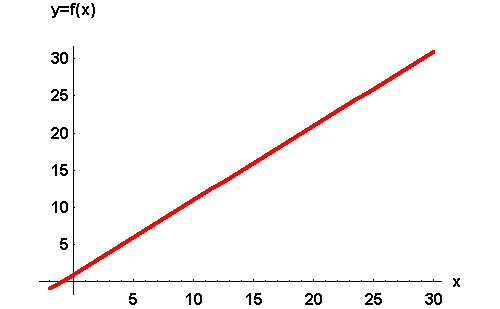
If the points (2, 3), (4, 5), (10, 11), and (25, 26) are located on the graph of a function, you could easily figure out a corresponding rule. To get the function value, you just add 1 to the first number. The rule is f(x) = x + 1.
|
The points (3, 8) and (3, 18) could not be points on the graph of a function because there are two different function values for the same x value.
To review exponential rules click on Exponential Rules.
To go straight to logarithms click on Logarithms.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus