Quadratic Polynomials: Completing the Square.
Quadratic Polynomials: Completing the Square.
If guessing does not work, "completing the square" will do the job.
.
We will actually consider the equivalent problem of finding the roots, the solutions of the equation
Move the constant term to the other side of the equation:
The magic trick of this method is to exploit the binomial formula:
If we look at the left side of the equation we want to solve, we see that it matches the first two terms of the binomial formula if b=1. Let's write down the binomial formula for b=1:
But the third term of the binomial formula does not show up in our equation; we make it show up by force by adding 1 to both sides of our equation:
This trick is called "completing the square"! Now we use the binomial formula to simplify the left side of our equation (also adding 7+1=8):
Next we take square roots of both sides, but be careful: there are two possible cases:
In both cases 
.
We are done, once we solve the two equations for x.
are the two roots of our polynomial. Consequently, our polynomial factors as follows:
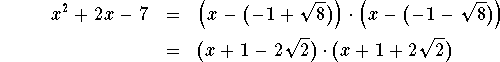
Let us try to factor 
.
We will again consider the equivalent problem of finding the roots, the solutions of the equation
In this example, the leading coefficient (the number in front of the 
) is 2, and thus not equal to 1; we can fix that by dividing by 2:
Move the constant term to the other side of the equation:
The magic trick of this method is to exploit the binomial formula:
If we look at the left side of the equation we want to solve, we see that it matches the first two terms of the binomial formula if b=3/2. Let's write down the binomial formula for b=3/2:
But the third term of the binomial formula does not show up in our equation; we make it show up by adding 
to both sides of our equation:
We have "completed the square"! Now we use the binomial formula to simplify the left side of our equation (also simplifying the right side):
The rest is easy: we take square roots of both sides, but be careful: there are two possible cases:
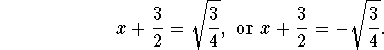
In both cases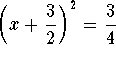 
.
We are done, once we solve the two equations for x.
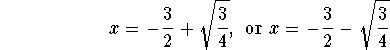
are the two roots of our polynomial. Here is the factorization of our polynomial. Be careful: We have to multiply our two "standard" factors by 2 (the leading term we divided by in the beginning!)
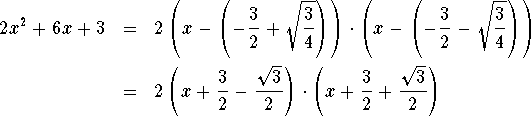
Let us factor 
.
We will again consider the equivalent problem of finding the roots, the solutions of the equation
Move the constant term to the other side of the equation:
The magic trick of this method is to exploit the binomial formula:
If we look at the left side of the equation we want to solve, we see that it matches the first two terms of the binomial formula if b=-3. You always take half of the term in front of the x. Let's write down the binomial formula for b=-3:
But the third term of the binomial formula does not show up in our equation; we make it show up by adding 9 to both sides of our equation:
We have "completed the square"! Now we use the binomial formula to simplify the left side of our equation (also simplifying the right side):
The rest is easy: we take square roots of both sides, but be careful: there are two possible cases:
In both cases 
.
We are done, once we solve the two equations for x.
are the two roots of our polynomial. Here is the factorization of our polynomial.
by completing the square.
by completing the square.
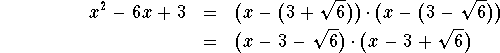
There are more exercises on the next page dealing with the quadratic formula.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Helmut Knaust