Factoring: Some Special Cases

The binomial formulas.

Here are three algebraic formulas, the binomial formulas, which can be used for factoring:

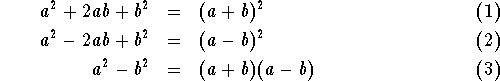
eqnarray11

You should check that these formulas work by multiplying out using the FOIL method.

Here is how to use these formulas for factoring purposes: Let's say we want to factor

We can write this polynomial as

and then notice that the terms match the second binomial formula for the values a=2x and b=3. Consequently,

and we have factored the polynomial completely. Note that x=3/2 is the only root, with multiplicity 2.

Here is another example: factor the polynomial

We can write the polynomial as the difference of two squares and then use the third binomial formula:

The cube of a binomial.

There are similar formulas to factor some special cubic polynomials:

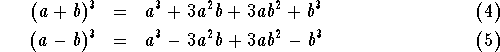
eqnarray23

As an example, let us factor the polynomial

We can rewrite this polynomial as

Now it matches formula (5) with a=2x and b=3. Consequently

The polynomial has a triple root at x=3/2.

Sums and differences of two cubes.

here are two more formulas to handle special cases of cubic polynomials:

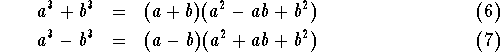
eqnarray26

Say, we like to factor . By formula (6), we can write

In this case the factorization is complete, since the polynomial is an irreducible quadratic polynomial.

What about the polynomial ? We first write this as the difference of two cubes, and then use formula (7):

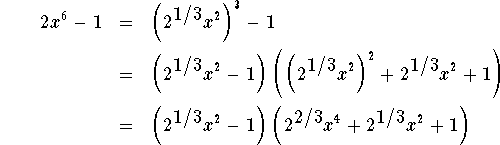
eqnarray29

Aside: Note that the factorization is still not complete. The Fundamental Theorem of Algebra tells us that it is possible to factor

further. Since you can see from the graph of this polynomial that it does not have real roots, the polynomial

can be factored into 2 irreducible quadratic polynomials. To find these two polynomials requires more familiarity with complex numbers; you can check that

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust

Factoring: Some Special Cases

The binomial formulas.

The cube of a binomial.

Sums and differences of two cubes.

Exercise 1.

Answer.

Exercise 2.

Answer.

Exercise 3.

Answer.

Exercise 4.

Answer.

Exercise 5.

Answer.